Expectation

기대값(expectation)은 보상(reward)과 그 보상을 받을 확률을 곱한 값의 총 합을 통해 얻을 수 있습니다. 즉, reward에 대한 가중합(weighted sum)라고 볼 수 있습니다. 주사위의 경우에는 reward의 경우에는 1부터 6까지 받을 수 있지만, 각 reward에 대한 확률은 ${1}/{6}$로 동일합니다.

$\begin{aligned} expected~reward~from~dice&=\sum^6_{x=1}{P(X=x)\times reward(x)} \\ where~P(x)=\frac{1}{6}, \forall x~~&and~~reward(x)=x. \end{aligned}$

따라서 실제 주사위의 기대값은 아래와 같이 3.5가 됩니다.

$\frac{1}{6}\times(1+2+3+4+5+6)=3.5$

또한, 위의 수식은 아래와 같이 표현 할 수 있습니다.

$\mathbb{E}_{X \sim P}[reward(x)]=\sum^6_{x=1}{P(X=x)\times reward(x)}=3.5$

주사위의 경우에는 discrete variable을 다루는 확률 분포이고, continuous variable의 경우에는 적분을 통해 우리는 기대값을 구할 수 있습니다.

Monte Carlo Sampling

Monte Carlo Sampling은 난수를 이용하여 임의의 함수를 근사하는 방법입니다. 예를 들어 임의의 함수 $f$가 있을 때, 사실은 해당 함수가 Gaussian distribution을 따르고 있고, 충분히 많은 수의 random number $x$를 생성하여, $f(x)$를 구한다면, $f(x)$의 분포는 역시 gaussian distribution을 따르고 있을 것 입니다. 이와 같이 임의의 함수에 대해서 Monte Carlo 방식을 통해 해당 함수를 근사할 수 있습니다.

따라서 Monte Carlo sampling을 사용하면 기대값(expectation) 내의 표현을 밖으로 꺼낼 수 있습니다. 즉, 주사위의 reward에 대한 기대값을 아래와 같이 간단히(simplify) 표현할 수 있습니다.

$\mathbb{E}_{X \sim P}[reward(x)] \approx \frac{1}{N}\sum^N_{i=1}{reward(x_i)}$

주사위 reward의 기대값은 $N$번 sampling한 주사위 값의 평균이라고 할 수 있습니다. 실제로 $N$이 무한대에 가까워질 수록 (커질 수록) 해당 값은 실제 기대값 $3.5$에 가까워질 것 입니다. 따라서 우리는 경우에 따라서 $N=1$인 경우도 가정 해 볼 수 있습니다. 즉, 아래와 같은 수식이 될 수도 있습니다.

$\mathbb{E}_{X \sim P}[reward(x)] \approx reward(x)=x$

위와 같은 가정을 가지고 수식을 간단히 표현할 수 있게 되면, 이후 gradient를 구한다거나 할 때에 수식이 간단해져 매우 편리합니다.

Policy Gradients

사실 강화학습(RL) 자체는 매우 유서 깊고 방대한 학문입니다. 따라서 이 책에서 깊은 내용을 모두 다루는 것은 어렵습니다. 우리는 NLP에 적용 가능한 방법에 대해서 그 개념을 간단히 다루고 넘어가도록 하겠습니다.

Policy Gradients는 정책기반 강화학습(Policy based Reinforcement Learning) 방식에 속합니다. 알파고를 개발했던 DeepMind에 의해서 유명해진 Deep Q-Learning은 가치기반 강화학습(Value based Reinforcement Learning) 방식에 속합니다. 실제 딥러닝을 사용하여 두 방식을 사용 할 때에 가장 큰 차이점은, Value based방식은 인공신경망을 사용하여 어떤 action을 하였을 때에 얻을 수 있는 보상을 예측 하도록 훈련하는 것과 달리, policy based 방식은 인공신경망은 어떤 action을 할지 훈련되고 해당 action에 대한 보상(reward)를 back-propagation 할 때에 gradient를 통해서 전달해 주는 것이 가장 큰 차이점 입니다. 따라서 어떤 Deep Q-learning의 경우에는 action을 선택하는 것이 deterministic한 것에 비해서, Policy Gradient 방식은 action을 선택 할 때에 stochastic한 process를 거치게 됩니다. Policy Gradient에 대한 수식은 아래와 같습니다.

$\pi_\theta(a|s) = P_\theta(a|s) = P(a|s; \theta)$

위의 $\pi$는 정책(policy)을 의미합니다. 즉, 신경망 $\theta$는 현재 상황(state) $s$가 주어졌을 때, 어떤 선택(action) $a$를 해야할 지 확률을 반환 합니다.

$\begin{aligned} J(\theta) &= \mathbb{E}_{\pi_\theta}[r] = v_\theta(s_0) \\ &=\sum_{s \in \mathcal{S}}{d(s)}\sum_{a \in \mathcal{A}}{\pi_\theta(s, a)\mathcal{R}_{s, a}} \end{aligned}$

우리의 목표(objective)는 최초 상황(initial state)에서의 기대누적보상(expected cumulative reward)을 최대(maximize)로 하도록 하는 policy($\theta$)를 찾는 것 입니다. 최소화 하여야 하는 손실(loss)와 달리 보상(reward)는 최대화 하여야 하므로 기존의 gradient descent 대신에 gradient ascent를 사용하여 최적화(optimization)을 수행 합니다.

$\theta_{t+1}=\theta_t+\alpha\triangledown_\theta J(\theta)$

Gradient ascent에 따라서, $\triangledown_\theta J(\theta)$를 구하여 $\theta$를 업데이트 해야 합니다. 여기서 $d(s)$는 markov chain의 stationary distribution으로써 시작점에 상관없이 전체의 trajecotry에서 $s$에 머무르는 시간의 proportion을 의미합니다.

$\begin{aligned} \triangledown_\theta\pi_\theta(s,a)&=\pi_\theta(s,a)\frac{\triangledown_\theta\pi_\theta(s,a)}{\pi_\theta(s,a)} \\ &=\pi_\theta(s,a)\triangledown_\theta\log{\pi_\theta(s,a)} \end{aligned}$

이때, 위의 로그 미분의 성질을 이용하여 아래와 같이 $\triangledown_\theta J(\theta)$를 구할 수 있습니다. 이 수식을 해석하면 매 time-step 별 상황($s$)이 주어졌을 때 선택($a$)할 로그 확률의 gradient에, 그에 따른 보상(reward)을 곱한 값의 기대값이 됩니다.

$\begin{aligned} \triangledown_\theta J(\theta)&=\sum_{s \in \mathcal{S}}{d(s)}\sum_{a \in \mathcal{A}}{\pi_\theta(s,a)}\triangledown_\theta\log{\pi_\theta(s, a)\mathcal{R}_{s,a}} \\ &= \mathbb{E}_{\pi_\theta}[\triangledown_\theta \log{\pi_\theta (a|s)}r] \end{aligned}$

Policy Gradient Theorem에 따르면, 여기서 해당 time-step에 대한 즉각적인 reward($r$) 대신에 episode의 종료까지의 총 reward, 즉 $Q$ function을 사용할 수 있습니다.

$\triangledown_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[\triangledown_\theta \log{\pi_\theta (a|s)}Q^{\pi_\theta}(s,a)]$

여기서 바로 Policy Gradients의 진가가 드러납니다. 우리는 policy network에 대해서 gradient를 구하지만, Q-function에 대해서는 gradient를 구할 필요가 없습니다. 즉, 미분의 가능 여부를 떠나서 임의의 어떠한 함수라도 보상 함수(reward function)로 사용할 수 있는 것입니다. 이렇게 어떠한 함수도 reward로 사용할 수 있게 됨에 따라, 기존의 단순히 cross entropy와 같은 손실 함수(loss function)에 학습(fitting) 시키는 대신에 좀 더 실제 문제에 부합하는 함수(번역의 경우에는 BLEU)를 사용하여 $\theta$를 훈련시킬 수 있게 되었습니다. 위의 수식에서 기대값 수식을 Monte Carlo sampling으로 대체하면 아래와 같이 parameter update를 수행 할 수 있습니다.

$\theta \leftarrow \theta + \alpha Q^{\pi_\theta}(s_t,a_t)\triangledown_\theta\log{\pi_\theta(a_t|s_t)}$

위의 수식을 좀 더 쉽게 설명 해 보면, Monte Carlo 방식을 통해 sampling 된 action들에 대해서 gradient를 구하고, 그 gradient에 reward를 곱하여 주는 형태입니다. 만약 샘플링 된 해당 action들이 좋은 (큰 양수) reward를 받았다면 learning rate $\alpha$에 추가적인 곱셈을 통해서 더 큰 step으로 gradient ascending을 할 수 있을 겁니다. 하지만 negative reward를 받게 된다면, gradient의 반대방향으로 step을 갖도록 값이 곱해지게 될 겁니다. 따라서 해당 샘플링 된 action들이 앞으로는 잘 나오지 않도록 parameter $\theta$가 update 됩니다.

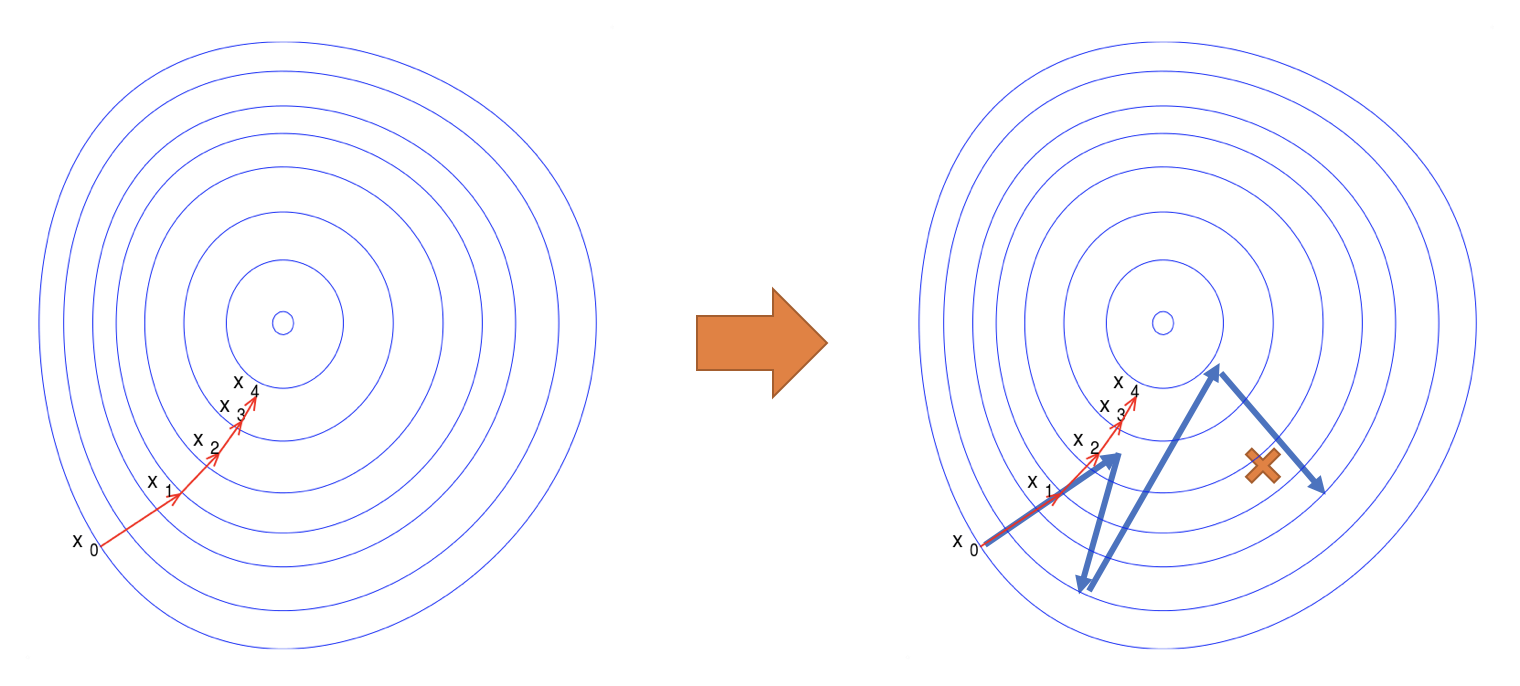
따라서 실제 gradient에 따른 local minima(지역최소점)를 찾는 것이 아닌, 아래 그림과 같이 실제 reward-objective function에 따른 최적을 값을 찾게 됩니다. 하지만, 기존의 gradient는 방향과 크기를 나타낼 수 있었던 것에 비해서, policy gradients는 기존의 gradient의 방향에 크기(scalar)값을 곱해줌으로써 방향을 직접 지정해 줄 수는 없습니다. 따라서 실제 목적함수(objective function)에 따른 최적의 방향을 스스로 찾아갈 수는 없습니다. 그러므로 사실 훈련이 어렵고 비효율적인 단점을 갖고 있습니다.

Policy Gradient에 대한 자세한 설명은 원 논문인 [Sutton at el.1999], 또는 해당 저자가 쓴 텍스트북 Reinforcement Learning: An Introduction[Sutton et al.2017]을 참고하거나, DeepMind David Silver의 YouTube 강의를 참고하면 좋습니다.

MLE vs RL(Policy Gradients)

여기서 reward의 역할을 좀 더 직관적으로 설명하고 넘어가도록 하겠습니다.

우리에게 $n$개의 시퀀스로 이루어진 입력을 받아, $m$개의 시퀀스로 이루어진 출력을 하는 함수를 근사하는 것이 목표로 주어진다고 가정 해 봅니다. 그렇다면 시퀀스 $X$와 $Y$는 $\mathcal{B}$라는 dataset에 존재 합니다.

$\begin{aligned} \mathcal{B} &= \{(X_i, Y_i)\}_{i=1}^{N}\\ X&=\{x_1, x_2, \cdots, x_n\} \\ Y&=\{y_0, y_1, \cdots, y_m\} \end{aligned}$

근사하여 얻은 함수는 임의의 시퀀스 $X$가 주어졌을 때, $\hat{Y}$를 반환하도록 잘 학습되어 있을 겁니다.

$\begin{aligned} \hat{Y}=argmax_{Y}P(Y|X) \end{aligned}$

그럼 해당 함수를 근사하기 위해서 우리는 parameter $\theta$를 학습해야 합니다. $\theta$는 아래와 같이 Maximum Likelihood Estimation(MLE)를 통해서 얻어질 수 있습니다.

$\begin{aligned} \hat{\theta}&=argmax_{\theta}P(\theta|X, Y) \\ &=argmax_{\theta}P(Y|X; \theta)P(\theta) \\ \end{aligned}$

$\theta$에 대해 MLE를 수행하기 위해서 우리는 목적함수(objective function)을 아래와 같이 정의 합니다. 아래는 cross entropy loss를 목적함수로 정의 한 것 입니다. 우리의 목표는 목적함수를 최소화(minimize)하는 것 입니다.

$\begin{aligned} J(\theta)&=-\frac{1}{N}\sum_{(X, Y) \in \mathcal{B}}{P(Y|X)\log{P(Y|X;\theta)}} \\ &=-\frac{1}{N}\sum_{(X, Y) \in \mathcal{B}}{\sum_{i = 0}^{m}{\log{P(y_i|X, y_{<i}; \theta)}}} \end{aligned}$

위의 수식에서 $P(Y|X)$는 훈련 데이터셋에 존재하므로 보통 $1$이라고 할 수 있습니다. 따라서 수식에서 생략 할 수 있습니다. 위에서 정의한 목적함수를 최소화 하여야 하기 때문에, gradient descent를 통해 지역최소점(local minima)를 찾아내어 전역최소점(global minima)에 근사(approximation)할 수 있습니다. 해당 수식은 아래와 같습니다.

$\begin{aligned} \theta &\leftarrow \theta - \gamma \nabla J(\theta) \\ \theta &\leftarrow \theta + \gamma \frac{1}{N}\sum_{(X, Y) \in \mathcal{B}}{\sum_{i = 0}^{m}{\nabla_\theta\log{P(y_i|X, y_{i}; \theta)}}} \end{aligned}$

우리는 위의 수식에서 learning rate $\gamma$를 통해 update step size를 조절 하는 것을 확인할 수 있습니다. 아래는 policy gradients에 기반하여 expected cumulative reward를 최대로 하는 gradient ascent 수식 입니다. Reward를 최대화(maximization)해야 하기 때문에 gradient acsent를 사용하는 것을 볼 수 있습니다.

$\begin{aligned} \theta &\leftarrow \theta + \alpha\nabla J(\theta) \\ \theta &\leftarrow \theta + \alpha Q^{\pi_\theta}(s_t,a_t)\triangledown_\theta\log{\pi_\theta(a_t|s_t)} \end{aligned}$

위의 수식에서도 이전 MLE의 gradient descent 수식과 마찬가지로, $\alpha$와 $Q^{\pi_\theta}(s_t,a_t)$가 gradient 앞에 붙어서 learning rate역할을 하는 것을 볼 수 있습니다. 따라서 reward에 따라서 해당 action들로부터 배우는 것을 더욱 강화하거나 반대방향으로 부정할 수 있는 것 입니다. 마치 좀 더 쉽게 비약적으로 설명하면 결과에 따라서 동적으로 learning rate를 알맞게 조절해 주는 것이라고 이해할 수 있습니다.

REINFORCE with baseline