PyTorch Short Tutorial
Tensor
PyTorch의 tensor는 numpy의 array와 같은 개념입니다. PyTorch 상에서 연산을 수행하기 위한 가장 기본적인 객체로써, 앞으로 우리가 수행할 모든 연산은 이 객체를 통하게 됩니다. 따라서 PyTorch는 tensor를 통해 값을 저장하고 그 값들에 대해서 연산을 수행할 수 있는 함수를 제공합니다.
아래의 예제는 같은 동작을 수행하는 PyTorch 코드와 NumPy 코드 입니다.
import torch
x = torch.Tensor(2, 2)
x = torch.Tensor([[1, 2], [3, 4]])
x = torch.from_numpy(x)
import numpy as np
x = [[1, 2], [3, 4]]
x = np.array(x)
보시다시피, PyTorch는 굉장히 NumPy와 비슷한 방식의 코딩 스타일을 갖고 있고, 따라서 코드를 보고 해석하거나 새롭게 작성함에 있어서 굉장히 수월합니다.
Tensor는 아래와 같이 다양한 자료형을 제공 합니다.
| Data type | dtype | CPU tensor | GPU tensor |
|---|---|---|---|
| 32-bit floating point | torch.float32 or torch.float | torch.FloatTensor | torch.cuda.FloatTensor |
| 64-bit floating point | torch.float64 or torch.double | torch.DoubleTensor | torch.cuda.DoubleTensor |
| 16-bit floating point | torch.float16 or torch.half | torch.HalfTensor | torch.cuda.HalfTensor |
| 8-bit integer (unsigned) | torch.uint8 | torch.ByteTensor | torch.cuda.ByteTensor |
| 8-bit integer (signed) | torch.int8 | torch.CharTensor | torch.cuda.CharTensor |
| 16-bit integer (signed) | torch.int16 or torch.short | torch.ShortTensor | torch.cuda.ShortTensor |
| 32-bit integer (signed) | torch.int32 or torch.int | torch.IntTensor | torch.cuda.IntTensor |
| 64-bit integer (signed) | torch.int64 or torch.long | torch.LongTensor | torch.cuda.LongTensor |
torch.Tensor를 통해 선언 하게 되면 디폴트 타입인 torch.FloatTensor로 선언하는 것과 같습니다.
좀 더 자세한 참고를 원한다면 PyTorch docs를 방문하시면 됩니다.
Autograd
PyTorch는 자동으로 미분 및 back-propagation을 해주는 Autograd 기능을 갖고 있습니다. 따라서 우리는 대부분의 tensor간의 연산들을 크게 신경 쓸 필요 없이 수행 하고, back-propagation을 수행하는 명령어를 호출 해 주기만 하면 됩니다.
이를 위해서, PyTorch는 tensor들 사이의 연산을 할 때마다 computational graph를 생성하여 연산의 결과물이 어떤 tensor로부터 어떤 연산을 통해서 왔는지 추적 하고 있습니다. 따라서 우리가 최종적으로 나온 스칼라(scalar)에 미분과 back-propagation(역전파)을 수행하도록 하였을 때, 자동으로 각 tensor 별로 자기 자신의 자식노드(child node)에 해당하는 tensor를 찾아서 계속해서 back-propagation 할 수 있도록 합니다.
import torch
x = torch.FloatTensor(2, 2)
y = torch.FloatTensor(2, 2)
y.requires_grad_(True)
z = (x + y) + torch.FloatTensor(2, 2)
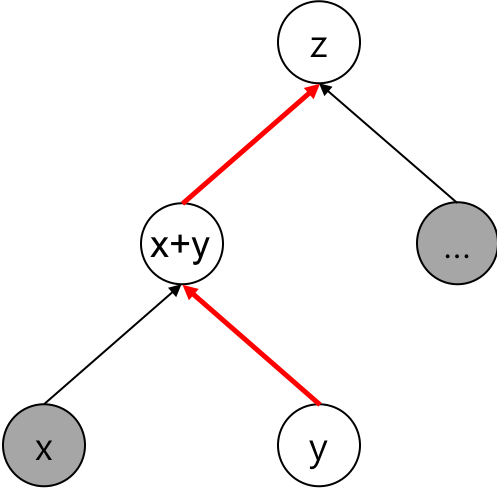
위의 예제에서처럼 와 를 생성하고 둘을 더하는 연산을 수행하면 , 이에 해당하는 tensor가 생성되어 computational graph에 할당 됩니다. 그리고 다시 생성 된 tensor를 더해준 뒤, 이를 에 assign(할당) 하게 됩니다. 따라서 로부터 back-propgation을 수행하게 되면, 이미 생성된 computational graph를 따라서 gradient를 전달 할 수 있게 됩니다.
Gradient를 구할 필요가 없는 연산의 경우에는 아래와 같이 with 문법을 사용하여 연산을 수행할 수 있습니다. back-propagation이 필요 없는 추론(inference) 등을 수행 할 때 유용하며, gradient를 구하기 위한 사전 작업들(computational graph 생성)을 생략할 수 있기 때문에, 연산 속도 및 메모리 사용에 있어서도 큰 이점을 지니게 됩니다.
import torch
with torch.no_grad():
x = torch.FloatTensor(2, 2)
y = torch.FloatTensor(2, 2)
y.requires_grad_(True)
z = (x + y) + torch.FloatTensor(2, 2)
How to Do Basic Operations (Forward)
이번에는 Linear Layer(또는 fully-connected layer, dense layer)를 구현 해 보도록 하겠습니다. M by N의 입력 matrix가 주어지면, N by P의 matrix를 곱한 후, P size의 vector를 bias로 더하도록 하겠습니다. 수식은 아래와 같을 것 입니다.
사실 이 수식에서 는 vector이지만, 보통 우리는 딥러닝을 수행 할 때에 mini-batch 기준으로 수행하므로, 가 matrix라고 가정 하겠습니다.
이를 좀 더 구현하기 쉽게 아래와 같이 표현 해 볼 수도 있습니다.
이러한 linaer layer의 기능은 아래와 같이 PyTorch로 구현할 수 있습니다.
import torch
def linear(x, W, b):
y = torch.mm(x, W) + b
return y
x = torch.FloatTensor(16, 10)
W = torch.FloatTensor(10, 5)
b = torch.FloatTensor(5)
y = linear(x, W, b)
Broadcasting
Broadcasting에 대해서 설명 해 보겠습니다. 역시 NumPy에서 제공되는 broadcasting과 동일하게 동작합니다. matmul()을 사용하면 임의의 차원의 tensor끼리 연산을 가능하게 해 줍니다. 이전에는 강제로 2차원을 만들거나 하여 곱해주는 수 밖에 없었습니다. 다만, 입력으로 주어지는 tensor들의 차원에 따라서 규칙이 적용됩니다. 그 규칙은 아래와 같습니다.
>>> # vector x vector
>>> tensor1 = torch.randn(3)
>>> tensor2 = torch.randn(3)
>>> torch.matmul(tensor1, tensor2).size()
-0.4334
[torch.FloatTensor of size ()]
>>> # matrix x vector
>>> tensor1 = torch.randn(3, 4)
>>> tensor2 = torch.randn(4)
>>> torch.matmul(tensor1, tensor2).size()
torch.Size([3])
>>> # batched matrix x broadcasted vector
>>> tensor1 = torch.randn(10, 3, 4)
>>> tensor2 = torch.randn(4)
>>> torch.matmul(tensor1, tensor2).size()
torch.Size([10, 3])
>>> # batched matrix x batched matrix
>>> tensor1 = torch.randn(10, 3, 4)
>>> tensor2 = torch.randn(10, 4, 5)
>>> torch.matmul(tensor1, tensor2).size()
torch.Size([10, 3, 5])
>>> # batched matrix x broadcasted matrix
>>> tensor1 = torch.randn(10, 3, 4)
>>> tensor2 = torch.randn(4, 5)
>>> torch.matmul(tensor1, tensor2).size()
torch.Size([10, 3, 5])
마찬가지로 덧셈 연산에 대해서도 broadcasting이 적용될 수 있는데 그 규칙은 아래와 같습니다. 곱셈에 비해서 좀 더 규칙이 복잡하니 주의해야 합니다.
>>> x=torch.FloatTensor(5,7,3)
>>> y=torch.FloatTensor(5,7,3)
# same shapes are always broadcastable (i.e. the above rules always hold)
>>> x=torch.FloatTensor()
>>> y=torch.FloatTensor(2,2)
# x and y are not broadcastable, because x does not have at least 1 dimension
# can line up trailing dimensions
>>> x=torch.FloatTensor(5,3,4,1)
>>> y=torch.FloatTensor( 3,1,1)
# x and y are broadcastable.
# 1st trailing dimension: both have size 1
# 2nd trailing dimension: y has size 1
# 3rd trailing dimension: x size == y size
# 4th trailing dimension: y dimension doesn't exist
# but:
>>> x=torch.FloatTensor(5,2,4,1)
>>> y=torch.FloatTensor( 3,1,1)
# x and y are not broadcastable, because in the 3rd trailing dimension 2 != 3
# can line up trailing dimensions to make reading easier
>>> x=torch.FloatTensor(5,1,4,1)
>>> y=torch.FloatTensor( 3,1,1)
>>> (x+y).size()
torch.Size([5, 3, 4, 1])
# but not necessary:
>>> x=torch.FloatTensor(1)
>>> y=torch.FloatTensor(3,1,7)
>>> (x+y).size()
torch.Size([3, 1, 7])
>>> x=torch.FloatTensor(5,2,4,1)
>>> y=torch.FloatTensor(3,1,1)
>>> (x+y).size()
RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1
Broadcasting 연산의 가장 주의해야 할 점은, 의도하지 않은 broadcasting연산으로 인해서 예상치 못한 버그가 발생할 가능성 입니다. 원래는 같은 크기의 tensor끼리 연산을 해야 하는 부분인데, 실수에 의해서 다른 크기가 되었을 때, 원래대로라면 덧셈 또는 곱셈을 하고 runtime error가 나서 알아차렸겠지만, broadcasting으로 인해서 runtime error가 나지 않고 의도치 않은 연산을 통해 프로그램이 정상적으로 종료 될 수 있습니다. 하지만 실행 결과로는 결국 기대하던 값과 다른 값이 나오게 되어, 이에 대한 원인을 찾느라 고생할 수도 있습니다. 따라서 주의가 필요합니다.
참고사이트:
nn.Module
이제까지 우리가 원하는 수식을 어떻게 어떻게 feed-forward 구현 하는지 살펴 보았습니다. 이것을 좀 더 편리하고 깔끔하게 사용하는 방법에 대해서 다루어 보도록 하겠습니다. PyTorch는 nn.Module이라는 class를 제공하여 사용자가 이 위에서 자신이 필요로 하는 model architecture를 구현할 수 있도록 하였습니다.
nn.Module의 상속한 사용자 정의 class는 다시 내부에 nn.Module을 상속한 class를 선언하여 소유 할 수 있습니다. 즉, nn.Module 안에 nn.Module 객체를 선언하여 사용 할 수 있습니다. 그리고 nn.Module의 forward() 함수를 override하여 feed-forward를 구현할 수 있습니다. 이외에도 nn.Module의 특성을 이용하여 한번에 weight parameter를 save/load할 수도 있습니다.
그럼 앞서 구현한 linear 함수 대신에 MyLinear라는 class를 nn.Module을 상속받아 선언하고, 사용하여 똑같은 기능을 구현 해 보겠습니다.
import torch
import torch.nn as nn
class MyLinear(nn.Module):
def __init__(self, input_size, output_size):
super(MyLinear, self).__init__()
self.W = torch.FloatTensor(input_size, output_size)
self.b = torch.FloatTensor(output_size)
def forward(self, x):
y = torch.mm(x, self.W) + self.b
return y
위와 같이 선언한 MyLinear class를 이제 직접 사용해서 정상 동작 하는지 확인 해 보겠습니다.
x = torch.FloatTensor(16, 10)
linear = MyLinear(10, 5)
y = linear(x)
forward()에서 정의 해 준대로 잘 동작 하는 것을 볼 수 있습니다. 하지만, 위와 같이 W와 b를 선언하면 문제점이 있습니다. parameters() 함수는 module 내에 선언 된 learnable parameter들을 iterative하게 주는 iterator를 반환하는 함수 입니다. 한번, linear module 내의 learnable parameter들의 크기를 size()함수를 통해 확인 해 보도록 하겠습니다.
>>> params = [p.size() for p in linear.parameters()]
>>> print(params)
[]
아무것도 들어있지 않은 빈 list가 찍혔습니다. 즉, linear module 내에는 learnable parameter가 없다는 이야기 입니다. 아래의 웹페이지에 그 이유가 자세히 나와 있습니다.
참고사이트: http://pytorch.org/docs/master/nn.html?highlight=parameter#parameters
A kind of Tensor that is to be considered a module parameter. Parameters are Tensor subclasses, that have a very special property when used with Module s - when they’re assigned as Module attributes they are automatically added to the list of its parameters, and will appear e.g. in parameters() iterator. Assigning a Tensor doesn’t have such effect. This is because one might want to cache some temporary state, like last hidden state of the RNN, in the model. If there was no such class as Parameter, these temporaries would get registered too.
따라서 우리는 Parameter라는 class를 사용하여 tensor를 wrapping해야 합니다. 그럼 아래와 같이 될 것 입니다.
class MyLinear(nn.Module):
def __init__(self, input_size, output_size):
super(MyLinear, self).__init__()
self.W = nn.Parameter(torch.FloatTensor(input_size, output_size), requires_grad = True)
self.b = nn.Parameter(torch.FloatTensor(output_size), requires_grad = True)
def forward(self, x):
y = torch.mm(x, self.W) + self.b
return y
그럼 아까와 같이 다시 linear module 내부의 learnable parameter들의 size를 확인 해 보도록 하겠습니다.
>>> params = [p.size() for p in linear.parameters()]
>>> print(params)
[torch.Size([10, 5]), torch.Size([5])]
잘 들어있는 것을 확인 할 수 있습니다. 그럼 깔끔하게 바꾸어 보도록 하겠습니다. 아래와 같이 바꾸면 제대로 된 구현이라고 볼 수 있습니다.
class MyLinear(nn.Module):
def __init__(self, input_size, output_size):
super(MyLinear, self).__init__()
self.linear = nn.Linear(input_size, output_size)
def forward(self, x):
y = self.linear(x)
return y
nn.Linear class를 사용하여 W와 b를 대체하였습니다. 그리고 아래와 같이 print를 해 보면 내부의 Linear Layer가 잘 찍혀 나오는 것을 확인 할 수 있습니다.
>>> print(linear)
MyLinear(
(linear): Linear(in_features=10, out_features=5, bias=True)
)
Backward (Back-propagation)
이제까지 원하는 연산을 통해 값을 앞으로 전달(feed-forward)하는 방법을 살펴보았습니다. 이제 이렇게 얻은 값을 우리가 원하는 값과의 차이를 계산하여 error를 뒤로 전달(back-propagation)하는 것을 해 보도록 하겠습니다.
예를 들어 우리가 원하는 값은 아래와 같이 이라고 하였을 때, linear의 결과값 matrix의 합과 목표값과의 거리(error 또는 loss)를 구하고, 그 값에 대해서 backward()함수를 사용함으로써 gradient를 구합니다. 이때, error는 sclar로 표현 되어야 합니다. vector나 matrix의 형태여서는 안됩니다.
objective = 100
x = torch.FloatTensor(16, 10)
linear = MyLinear(10, 5)
y = linear(x)
loss = (objective - y.sum())**2
loss.backward()
위와 같이 구해진 각 parameter들의 gradient에 대해서 gradient descent 방법을 사용하여 error(loss)를 줄여나갈 수 있을 것 입니다.
train() and eval()
# Training...
linear.eval()
# Do some inference process.
linear.train()
# Restart training, again.
위와 같이 PyTorch는 train()과 eval() 함수를 제공하여 사용자가 필요에 따라 model에 대해서 훈련시와 추론시의 모드 전환을 쉽게 할 수 있도록 합니다. nn.Module을 상속받아 구현하고 생성한 객체는 기본적으로 training mode로 되어 있는데, eval()을 사용하여 module로 하여금 inference mode로 바꾸어주게 되면, (gradient를 계산하지 않도록 함으로써) inference 속도 뿐만 아니라, dropout 또는 batch-normalization과 같은 training과 inference 시에 다른 forward() 동작을 하는 module들에 대해서 각기 때에 따라 올바른 동작을 하도록 합니다. 다만, inference가 끝나면 다시 train()을 선언 해 주어, 원래의 훈련모드로 돌아가게 해 주어야 합니다.
Example
이제까지 배운 것들을 활용하여 임의의 함수를 근사(approximate)하는 신경망을 구현 해 보도록 하겠습니다.
- Random(임의)으로 생성한 tensor들을
- 우리가 근사하고자 하는 정답 함수에 넣어 정답을 구하고,
- 그 정답()과 신경망을 통과한 과의 차이(error)를 Mean Square Error(MSE)를 통해 구하여
- SGD를 통해서 최적화(optimize)하도록 해 보겠습니다.
MSE의 수식은 아래와 같습니다.
먼저 1개의 linear layer를 가진 MyModel이라는 모듈(module)을 선언합니다.
import random
import torch
import torch.nn as nn
class MyModel(nn.Module):
def __init__(self, input_size, output_size):
super(MyModel, self).__init__()
self.linear = nn.Linear(input_size, output_size)
def forward(self, x):
y = self.linear(x)
return y
그리고 아래와 같이, 임의의 함수가 동작한다고 가정하겠습니다.
해당 함수를 python으로 구현하면 아래와 같습니다. 물론 신경망 입장에서는 내부 동작 내용을 알 수 없는 함수 입니다.
def ground_truth(x):
return 3 * x[:, 0] + x[:, 1] - 2 * x[:, 2]
아래는 입력을 받아 feed-forward 시킨 후, back-propagation하여 gradient descent까지 하는 함수 입니다.
def train(model, x, y, optim):
# initialize gradients in all parameters in module.
optim.zero_grad()
# feed-forward
y_hat = model(x)
# get error between answer and inferenced.
loss = ((y - y_hat)**2).sum() / x.size(0)
# back-propagation
loss.backward()
# one-step of gradient descent
optim.step()
return loss.data[0]
그럼 위의 함수들을 사용 하기 위해서 하이퍼 파라미터(hyper-parameter)를 설정 하겠습니다.
batch_size = 1
n_epochs = 1000
n_iter = 10000
model = MyModel(3, 1)
optim = torch.optim.SGD(model.parameters(), lr = 0.0001, momentum=0.1)
print(model)
위의 값을 사용하여 평균 손실(loss)값이 보다 작을 때 까지 훈련 시킵니다.
for epoch in range(n_epochs):
avg_loss = 0
for i in range(n_iter):
x = torch.rand(batch_size, 3)
y = ground_truth(x.data)
loss = train(model, x, y, optim)
avg_loss += loss
avg_loss = avg_loss / n_iter
# simple test sample to check the network.
x_valid = torch.FloatTensor([[.3, .2, .1]])
y_valid = ground_truth(x_valid.data)
model.eval()
y_hat = model(x_valid)
model.train()
print(avg_loss, y_valid.data[0], y_hat.data[0, 0])
if avg_loss < .001: # finish the training if the loss is smaller than .001.
break
위와 같이 임의의 함수에 대해서 실제로 신경망을 근사(approximate)하는 아주 간단한 예제를 살펴 보았습니다. 사실은 신경망이라기보단, 선형 회귀(linear regression) 함수라고 봐야 합니다. 하지만, 앞으로 책에서 다루어질 구조(architecture)들과 훈련 방법들도 이 예제의 연장선상에 지나지 않습니다.
이제까지 다룬 내용을 바탕으로 PyTorch상에서 딥러닝을 수행하는 과정은 아래와 같이 요약 해 볼 수 있습니다.
- nn.Module 클래스를 상속받아 Model 아키텍쳐 선언(forward함수를 통해)
- Model 객체 생성
- SGD나 Adam등의 Optimizer를 생성하고, Model의 parameter를 등록
- 데이터로 미니배치를 구성하여 feed-forward --> computation graph 생성
- 손실함수(loss function)를 통해 최종 결과값(scalar) loss를 계산
- 손실(loss)에 대해서 backward() 호출 --> computation graph 상의 tensor들에 gradient가 채워짐
- 3번의 optimizer에서 step()을 호출하여 gradient descent 1-step 수행
Using GPU
PyTorch는 당연히 GPU상에서 훈련하는 방법도 제공합니다. 아래와 같이 cuda()함수를 통해서 원하는 객체를 GPU memory상으로 copy(Tensor의 경우)하거나 move(nn.Module의 하위 클래스인 경우) 시킬 수 있습니다.
>>> # Note that tensor is declared in torch.cuda.
>>> x = torch.cuda.FloatTensor(16, 10)
>>> linear = MyLinear(10, 5)
>>> # .cuda() let module move to GPU memory.
>>> linear.cuda()
>>> y = linear(x)
또한, cpu()함수를 통해서 다시 PC의 memory로 copy하거나 move할 수 있습니다.