Dual Unsupervised Learning

Dual Learning for Machine Translation

공교롭게도 CycleGAN과 비슷한 시기에 나온 논문[Xia at el.2016]이 있습니다. NLP의 특성상 CycleGAN처럼 직접적으로 gradient를 전달해 줄 수는 없었지만 기본적으로는 아주 비슷한 개념입니다. 짝이 없는 단방향(monolingual) corpus를 이용하여 성능을 극대화 하고자 하였습니다.

즉, monolingual sentence($s$)에 대해서 번역을 하고 그 문장($s_{mid}$)을 사용하여 복원을 하였을 때($\hat{s}$) 원래의 처음 문장으로 돌아올 수 있도록(처음 문장과의 차이를 최소화 하도록) 훈련하는 것입니다. 이때, 번역된 문장 $s_{mid}$는 자연스러운 해당 언어의 문장이 되었는가도 중요한 지표가 됩니다.

위에서 설명한 알고리즘을 따라가 보겠습니다. 이 방법에서는 $Set~X,~Set~Y$ 대신에 $Language~A,~Language~B$로 표기하고 있습니다. $G_{A \rightarrow B}$의 파라미터 $\theta_{AB}$와 $F_{B \rightarrow A}$의 파라미터 $\theta_{BA}$가 등장합니다. 이 $G_{A \rightarrow B}, F_{B \rightarrow A}$는 모두 parallel corpus에 의해서 pre-training이 되어 있는 상태 입니다. 즉, 기본적인 저성능의 번역기 수준이라고 가정합니다.

우리는 기존의 policy gradient와 마찬가지로 아래와 같은 파라미터 업데이트를 수행해야 합니다.

$\begin{aligned} \theta_{AB} \leftarrow \theta_{AB} + \gamma \triangledown_{\theta_{AB}}\hat{\mathbb{E}}[r] \\ \theta_{BA} \leftarrow \theta_{BA} + \gamma \triangledown_{\theta_{BA}}\hat{\mathbb{E}}[r] \end{aligned}$

$\hat{\mathbb{E}}[r]$을 각각의 파라미터에 대해서 미분 해 준 값을 더해주는 것을 볼 수 있습니다. 이 reward의 기대값은 아래와 같이 구할 수 있습니다.

$\begin{aligned} r&=\alpha r_{AB} + (1-\alpha)r_{BA} \\ r_{AB}&=LM_{B}(s_{mid}) \\ r_{BA}&=\log{P(s|s_{mid};\theta_{BA})} \\ \end{aligned}$

위와 같이 $k$개의 sampling한 문장에 대해서 각기 방향에 대한 reward를 각각 구한 후, 이를 선형 결합(linear combination)을 취해줍니다. 이때, $s_{mid}$는 sampling한 문장을 의미하고, $LM_B$를 사용하여 해당 문장이 $language B$의 집합에 잘 어울리는지를 따져 reward로 리턴합니다. 여기서 기존의 cross entropy를 사용할 수 없는 이유는 monlingual sentence이기 때문에 번역을 하더라도 정답을 알 수 없기 때문입니다. 또한 우리는 다수의 단방향(monolingual) corpus를 갖고 있기 때문에, $LM$은 쉽게 만들어낼 수 있습니다.

$\begin{aligned} \triangledown_{\theta_{AB}}\hat{\mathbb{E}}[r]&=\frac{1}{K}\sum_{k=1}^K{[r_k\triangledown_{\theta_{AB}}\log{P(s_{mid,k}|s;\theta_{AB})}]} \\ \triangledown_{\theta_{BA}}\hat{\mathbb{E}}[r]&=\frac{1}{K}\sum_{k=1}^K[(1-\alpha)\triangledown_{\theta_{BA}}\log{P(s|s_{mid,k};\theta_{BA})}] \end{aligned}$

이렇게 얻어진 $\mathbb{E}[r]$를 각 파라미터에 대해서 미분하게 되면 위와 같은 수식을 얻을 수 있고, 상기 서술한 파라미터 업데이트 수식에 대입하면 됩니다. 비슷한 방식으로 $B \rightarrow A$를 구할 수 있습니다.

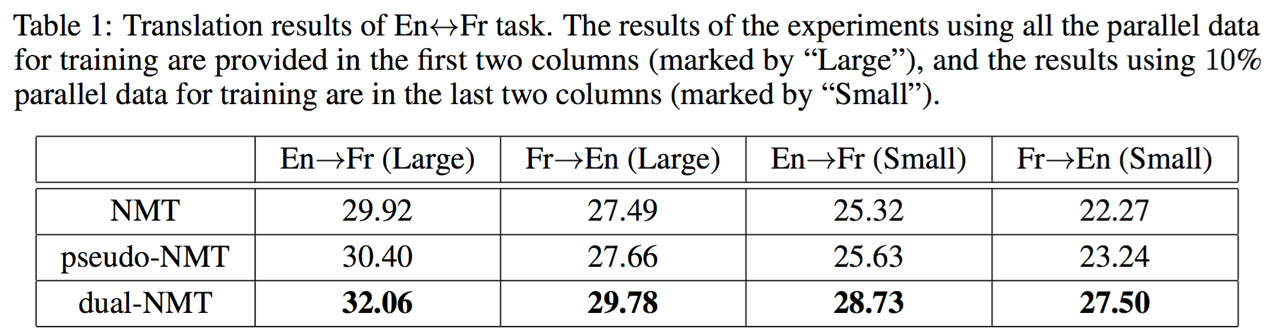
위의 테이블은 이 방법의 성능을 비교한 결과 입니다. Pseudo-NMT는 이전 챕터에서 설명하였던 back-translation을 의미합니다. 그리고 그 방식보다 더 좋은 성능을 기록한 것을 볼 수 있습니다.

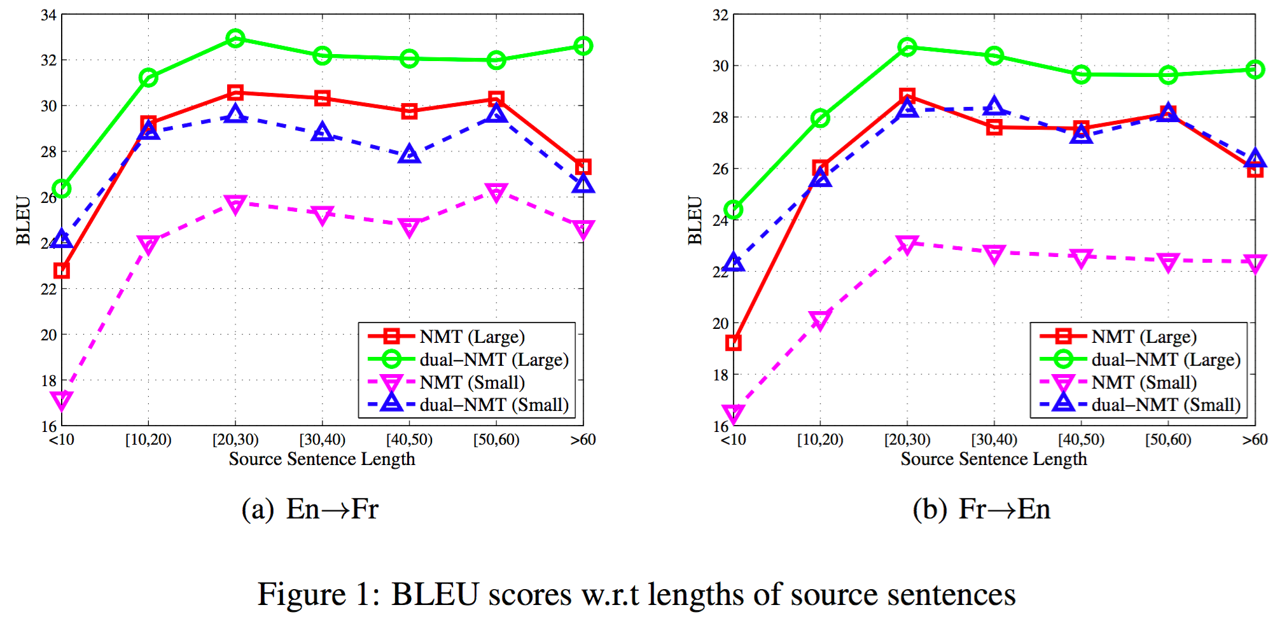
또한, 위 그래프에서 문장의 길이와 상관 없이 모든 구간에서 baseline NMT를 성능으로 압도하고 있는 것을 알 수 있습니다. 다만, 병렬(parallel) corpus의 양이 커질수록 단방향(monolingual) corpus에 의한 성능 향상의 폭이 줄어드는 것을 확인 할 수 있습니다.

이 방법은 강화학습과 Duality를 접목하여 적은 양의 병렬(parallel) corpus와 다수의 단방향(monolingual) corpus를 활용하여 번역기의 성능을 효과적으로 끌어올리는 방법을 제시하였다는 점에서 주목할 만 합니다.

Dual Transfer Learning for NMT with Marginal Distribution Regularization

Dual Supervised Learning (DSL)은 베이즈 정리에 따른 수식을 제약조건으로 사용하였다면, 이 방법[Wang et al.2017]은 Marginal 분포(distribution)의 성질을 이용하여 제약조건을 만듭니다.

Marginal Distribution from Wikipedia

$P(y)=\sum_{x \in \mathcal{X}}{P(x,y)}=\sum_{x \in \mathcal{X}}{P(y|x)P(x)}$

Marginal 분포는 결합확률분포(joint distribution)를 어떤 한 variable에 대해서 합 또는 적분 한 것을 이릅니다. 이것을 조건부확률로 나타낼 수 있고, 여기서 한발 더 나아가 기대값 표현으로 바꿀 수 있습니다. 그리고 이를 $K$번 샘플링 하도록 하여 Monte Carlo로 근사 표현 할 수 있습니다.

$\begin{aligned} p(y)=\sum_{x \in \mathcal{X}}{P(y|x;\theta)P(x)}&=\mathbb{E}_{x \sim P(x)}P(y|x;\theta) \\ &\approx\frac{1}{K}\sum^K_{i=1}{P(y|x^i;\theta)},~x^i\sim P(x) \end{aligned}$

이제 위의 수식을 기계번역에 적용해 보도록 하겠습니다. 우리에게 아래와 같이 $N$개의 source 문장 $x$, target 문장 $y$으로 이루어진 양방향 corpus $\mathcal{B}$, $S$개의 target 문장 $y$로만 이루어진 단방향 corpus $\mathcal{M}$이 있다고 가정 해 보겠습니다.

$\begin{aligned} \mathcal{B}&=\{(x^n, y^n)\}^N_{n=1} \\ \mathcal{M}&=\{y^s\}^S_{s=1} \end{aligned}$

그럼 우리는 아래의 목적함수(objective function)을 최대화(maximize)하는 동시에 marginal 분포에 따른 제약조건 또한 만족시켜야 합니다.

$\begin{aligned} &Objective: \sum^N_{n=1}{\log{P(y^n|x^n;\theta)}}, \\ &s.t.~P(y)=\mathbb{E}_{x\sim P(x)}P(y|x;\theta), \forall{y}\in\mathcal{M}. \end{aligned}$

위의 수식을 DSL과 마찬가지로 Lagrange multipliers와 함께 기존의 손실함수(loss function)에 추가하여 주기 위하여 $S(\theta)$와 같이 표현합니다.

$\mathcal{S}(\theta)=[\log\hat{P}(y)-\log{\mathbb{E}_{x\sim\hat{P}(x)}P(y|x;\theta)}]^2$

$\mathcal{L}(\theta)=-\sum^N_{n=1}{\log{P(y^n|x^n;\theta)}}+\lambda\sum^S_{s=1}{[\log\hat{P}(y)-\log{\mathbb{E}_{x\sim\hat{P}(x)}P(y|x;\theta)}]^2}$

이때, DSL과 유사하게 $\hat{P}(x)$와 $\hat{P}(y)$가 등장합니다. $\hat{P}(y)$는 단방향(monolingual) corpus로 만든 언어모델(language model)을 통해 확률값을 구합니다. 위의 수식에 따르면 $\hat{P}(x)$를 통해 source 문장 $x$를 샘플링(sampling)하여 네트워크 $\theta$를 통과시켜 $P(y|x;\theta)$를 구해야겠지만, 아래와 같이 좀 더 다른 방법으로 접근합니다.

$\begin{aligned} P(y)=\mathbb{E}_{x\sim\hat{P}(x)}P(y|x;\theta)&=\sum_{x\in\mathcal{X}}{P(y|x;\theta)\hat{P}(x)} \\ &=\sum_{x\in\mathcal{X}}\frac{P(y|x;\theta)\hat{P}(x)}{P(x|y)}P(x|y) \\ &=\mathbb{E}_{x\sim P(x|y)}\frac{P(y|x;\theta)\hat{P}(x)}{P(x|y)} \\ &=\frac{1}{K}\sum^K_{i=1}{\frac{P(y|x_i;\theta)\hat{P}(x_i)}{P(x_i|y)}}, x_i\sim P(x|y) \end{aligned}$

위와 같이 target 문장 $y$를 반대 방향 번역기($y \rightarrow x$)에 넣어 $K$개의 source 문장 $x$를 샘플링(sampling)하여 $P(y)$를 구합니다. 이 과정을 다시 하나의 손실함수(loss function)으로 표현하면 아래와 같습니다.

$\mathcal{L}(\theta)\approx-\sum^N_{n=1}{\log{P(y^n|x^n;\theta)}}+\lambda\sum^S_{s=1}{[\log{\hat{P}(y^s)}-\log{\frac{1}{K}\sum^K_{i=1}\frac{\hat{P}(x^s_i)P(y^s|x^s_i\theta)}{P(x^s_i|y^s)}}]^2}$

위의 테이블과 같이, 이 방법은 앞 챕터에서 소개한 기존의 단방향 corpus[Gulcehre et al.2015][Sennrich et al.2016]를 활용한 방식들과 비교하여 훨씬 더 나은 성능의 개선을 보여주었으며, 바로 앞서 소개한 Dual Learning[He et al.2016a]보다도 더 나은 성능을 보여줍니다. 마찬가지로, 불안정하고 비효율적인 강화학습을 사용하지 않고도 더 나은 성능을 보여준 것은 주목할 만한 성과라고 할 수 있습니다.